Why Plastic Viscosity = 600rpm – 300rpm reading
If you’ve ever worked with drilling fluids, you’ve probably heard — or even used — the shortcut:
But have you ever asked: why? Where does this come from? Is it just a field trick, or is there solid fluid mechanics behind it.
In this post, we’ll start from the basics of fluid behavior, explore how the viscometer works, and derive the equation step-by-step until we land at that simple but powerful rule: PV = 600 – 300
This formula seems empirical at first glance, but it’s actually rooted in fluid mechanics and rheology, particularly from the Bingham Plastic Model.
Rheology is the study of how fluids flow and deform under force. For drilling fluids, it describes how the mud behaves when pumped through the wellbore.
Plastic Viscosity (PV) is a key rheological property that represents the mud’s internal friction during flow. It tells us how “thick” the mud behaves while circulating.
How We Measure Rheology:
We use a rotational viscometer (like the Fann VG Meter), which spins a sleeve in the mud and measures the torque needed to maintain rotation at specific speeds (RPMs). The torque is converted to dial readings, which reflect the shear stress applied at different shear rates.
How the Bingham Plastic Model Helps:
Drilling fluids don’t behave like water — their flow is more complex. The Bingham Plastic Model , illustrated in the figure, simplifies this behavior using a linear equation:
τ = Shear stress
τy = Yield stress
μp = Plastic viscosity
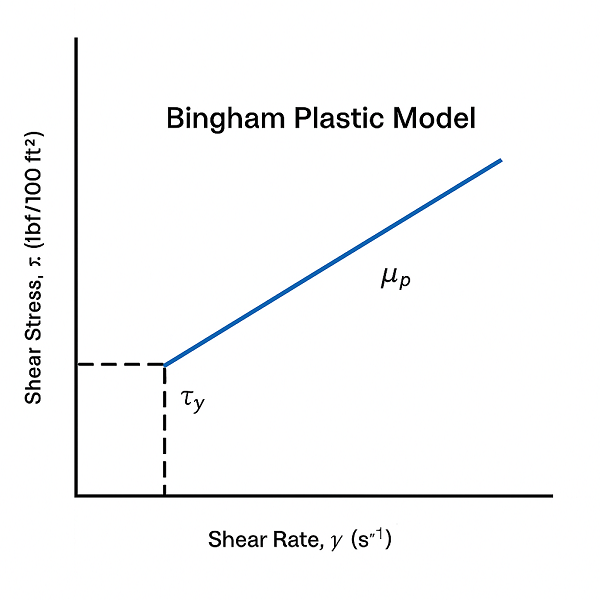
Deriving PV from the Bingham Model:
The plastic viscosity is the slope of the Bingham line:
At 600 rpm (γ~1022 s-1) and At 300 rpm (γ~511 s-1):
But PV is reported in centipoise (cP), and due to the unit conversions (lb/100 ft2), the factor simplifies to:
Since 1 lb/100 ft2= 478.8 cp. S-1, we adjust the units:
Thus, the field approximation :
If this helped you, consider donating $1 via E-transfer to syeds@hotmail.com with security code 129. Thank you! 🙏
Thanks for sharing
you’re welcome Soliman
Thanks
you’re welcome Djem
what you failed to explain is that the rotor bob dimensions ratio (1.0678) and spring constant for the Fann type direct indicating rotational viscometer gives the 1 dial degree of shear stress equals 1.067 lbf/100 ft2 and that is what make the simple calculations work PV = 600-300 and YP = PV-300
see example in https%3A%2F%2Farxiv.org%2Fpdf%2F2308.04975&usg=AOvVaw3QRlYpAmkSXM6o0GvQxujH&opi=89978449
Paul Scott,
Thank you for your feedback—you are absolutely correct. To clarify, I accounted for that factor in the relevant equations by multiplying 1.067 by both 600 RPM and 300 RPM.
Additionally, I would be delighted to collaborate further. If you have suggestions for revisions to the existing blog or ideas for a new article you’d like to publish, please feel free to share them. I would be happy to publish your work on my website with full attribution to you as the author.